Trong những năm gần đây, việc chuẩn bị cho phỏng vấn lập trình đã trở nên khó khăn hơn. Do đó, nếu chúng ta chỉ ôn lại vài cấu trúc dữ liệu cơ bản và làm một số bài luyện tập thì tỷ lệ phỏng vấn thành công rất thấp . Trong bài viết này, tôi sẽ chia sẻ chiến lược mà tôi thường dùng để chuẩn bị cho vòng phỏng vấn lập trình.
Tôi đã làm Software Engineer được khoảng 15 năm và đã đổi công việc năm lần. Tôi đã tham gia khoảng 120 cuộc phỏng vấn, và còn có cơ hội ngồi ở vị trí người tuyển dụng trong hơn 200 buổi phỏng vấn techincal và 100 buổi phỏng vấn system design.
Mặc dù tôi tự thấy mình là một kỹ sư có tố chất giỏi, nhưng tôi vẫn gặp khó khăn khi phải giải các bài toán lập trình trên bảng trắng, nhất là khi bị đánh giá trong một buổi phỏng vấn. Để vượt qua điều này, tôi đã dành nhiều thời gian cho việc chuẩn bị và luyện tập. Tôi có một quy trình rõ ràng: mỗi ngày làm khoảng 12–15 bài trong vòng 2 giờ. Nhờ đó, tôi giải được hơn 350 bài toán trong một tháng. Nhờ phương pháp này, tôi đã thành công trong các buổi phỏng vấn với các công ty lớn như FAANG (Facebook, Apple, Amazon, Netflix, Google).
Làm sao tôi có thể luyện tập hơn 12 bài mỗi ngày trong khi vẫn đi làm toàn thời gian?
Thay vì chỉ tập trung giải bài toán, tôi cố gắng liên kết bài toán mới với những bài tôi đã từng giải. Khi đọc đề, tôi sẽ dành vài phút để tìm xem mình có gặp bài nào tương tự chưa. Nếu có, tôi sẽ tập trung vào các yêu cầu khác biệt. Nếu gặp bài hoàn toàn mới, tôi sẽ thử giải rồi tìm hiểu thêm xem người khác làm thế nào. Dần dần, tôi đã xây dựng được một bộ các mẫu bài toán, giúp tôi dễ dàng nhận ra điểm tương đồng giữa bài mới và những bài đã biết. Dưới đây là một số ví dụ:
-
Nếu input đã được sắp xếp (mảng, danh sách, hoặc ma trận), ta sẽ dùng biến thể của Tìm kiếm Nhị phân (Binary Search) hoặc chiến lược Hai Con Trỏ (Two Pointers).
-
Nếu cần tìm top k phần tử lớn nhất/nhỏ nhất/gần nhất trong số n phần tử, ta sẽ dùng Heap.
-
Nếu cần thử hết tất cả các tổ hợp hoặc hoán vị của input, ta có thể dùng Backtracking đệ quy hoặc Tìm kiếm theo chiều rộng (BFS).
Nhờ cách tiếp cận dựa trên mẫu này, tôi tiết kiệm được rất nhiều thời gian chuẩn bị. Khi quen với một mẫu, bạn sẽ có thể giải được nhiều bài tương tự. Ngoài ra, chiến lược này cũng giúp tôi tự tin hơn khi gặp phải những bài toán lạ, vì tôi đã có thói quen liên kết bài mới với bài đã biết.
Trong phần còn lại của bài viết, tôi sẽ chia sẻ các mẫu bài toán mà tôi đã thu thập và đưa ra một số ví dụ. Để tìm hiểu chi tiết hơn về những vấn đề này và các cách giải, bạn có thể tham khảo "Grokking the Coding Interview."
 |
 |
 |
 |
 |
 |
 |
 |
|
|
 |
1. Bài toán mẫu: Tìm K điểm gần gốc tọa độ nhất
Đề bài: Cho một mảng các điểm trên mặt phẳng 2D, hãy tìm K điểm gần nhất so với gốc tọa độ.
Example: Input: points = [[1,2],[1,3]], K = 1, Output: [[1,2]]
|
Giải pháp: Khoảng cách Euclid từ một điểm P(x, y) đến gốc tọa độ có thể được tính bằng công thức sau:
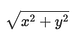
Chúng ta có thể sử dụng Max Heap để tìm K điểm gần gốc tọa độ nhất. Đầu tiên, ta sẽ đưa K điểm đầu tiên vào trong heap. Sau đó, khi duyệt qua các điểm còn lại, nếu có điểm nào (gọi là P) gần gốc tọa độ hơn so với điểm đang nằm trên đỉnh của heap, ta sẽ loại bỏ điểm trên đỉnh ra và thêm P vào. Cách này giúp chúng ta luôn giữ lại những điểm gần gốc tọa độ nhất trong heap.
Thuật toán của chúng ta sẽ trông như sau:
class Point { |
int x; |
int y; |
public Point(int x, int y) { |
this.x = x; |
this.y = y; |
} |
public int distFromOrigin() { |
// ignoring sqrt |
return (x * x) + (y * y); |
} |
} |
class KClosestPointsToOrigin { |
public static List<Point> findClosestPoints(Point[] points, int k) { |
PriorityQueue<Point> maxHeap = new PriorityQueue<>( |
(p1, p2) -> p2.distFromOrigin() - p1.distFromOrigin()); |
// put first 'k' points in the max heap |
for (int i = 0; i < k; i++) |
maxHeap.add(points[i]); |
// go through the remaining points of the input array, if a point is closer to |
// the origin than the top point of the max-heap, remove the top point from |
// heap and add the point from the input array |
for (int i = k; i < points.length; i++) { |
if (points[i].distFromOrigin() < maxHeap.peek().distFromOrigin()) { |
maxHeap.poll(); |
maxHeap.add(points[i]); |
} |
} |
// the heap has 'k' points closest to the origin, return them in a list |
return new ArrayList<>(maxHeap); |
} |
public static void main(String[] args) { |
Point[] points = new Point[] { new Point(1, 3), new Point(3, 4), new Point(2, -1) }; |
List<Point> result = KClosestPointsToOrigin.findClosestPoints(points, 2); |
System.out.print("Here are the k points closest the origin: "); |
for (Point p : result) |
System.out.print("[" + p.x + " , " + p.y + "] "); |
} |
} |
2. Bài toán mẫu cho Mẹo 3: Tập hợp
Đề bài: Cho một tập hợp với các phần tử khác nhau, hãy tìm tất cả các tập con khác nhau của nó.
Example: Input: [1, 5, 3]
|
Giải pháp: Chúng ta có thể sử dụng phương pháp Duyệt Theo Chiều Rộng (Breadth-First Search - BFS) để tạo ra tất cả các tập con của tập hợp đã cho. Bắt đầu với một tập rỗng, sau đó lần lượt duyệt qua từng phần tử và thêm chúng vào các tập con hiện có để tạo ra các tập con mới.
Hãy cùng xem qua ví dụ sau để hiểu rõ từng bước của thuật toán:
-
Tập hợp cho trước: [1, 5, 3]
-
Bắt đầu với tập rỗng: [[]]
-
Thêm số đầu tiên (1) vào tất cả các tập con hiện có để tạo ra các tập con mới: [[], [1]]
-
Thêm số thứ hai (5) vào tất cả các tập con hiện có: [[], [1], [5], [1,5]]
-
Thêm số thứ ba (3) vào tất cả các tập con hiện có: [[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3]]
Dưới đây là minh họa các bước trên:
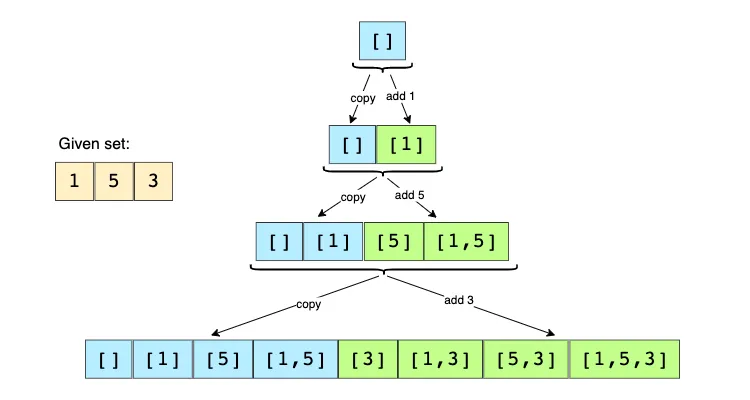
Thuật toán của chúng ta sẽ trông như sau:
class Subsets { |
public static List<List<Integer>> findSubsets(int[] nums) { |
List<List<Integer>> subsets = new ArrayList<>(); |
// start by adding the empty subset |
subsets.add(new ArrayList<>()); |
for (int currentNumber : nums) { |
// we will take all existing subsets and insert the current number in them to |
// create new subsets |
int n = subsets.size(); |
for (int i = 0; i < n; i++) { |
// create a new subset from the existing subset and |
// insert the current element to it |
List<Integer> set = new ArrayList<>(subsets.get(i)); |
set.add(currentNumber); |
subsets.add(set); |
} |
} |
return subsets; |
} |
public static void main(String[] args) { |
List<List<Integer>> result = Subsets.findSubsets(new int[] { 1, 3 }); |
System.out.println("Here is the list of subsets: " + result); |
result = Subsets.findSubsets(new int[] { 1, 5, 3 }); |
System.out.println("Here is the list of subsets: " + result); |
} |
} |
Lời kết
Nhờ vào những mẫu này, tôi đã tiết kiệm được nhiều thời gian khi chuẩn bị cho phỏng vấn lập trình. Bạn có thể tham khảo "Grokking the Coding Interview" để tìm thêm nhiều mẫu và bài toán mẫu khác.
Ngoài ra, hãy xem "Grokking the System Design Interview" và "Grokking the Advanced System Design Interview" để tìm một số ví dụ hay về các câu hỏi thiết kế hệ thống và câu trả lời cho chúng.
Nguồn: Arslan Ahmad
TẠO TÀI KHOẢN MỚI: XEM FULL “1 TÁCH CODEFEE” - NHẬN SLOT TƯ VẤN CV TỪ CHUYÊN GIA - CƠ HỘI RINH VỀ VOUCHER 200K